Looginen pähkinäallergia

Olen lapsesta saakka ollut kiinnostunut erilaisista päättelytehtävistä. Suunnilleen yhtä kauan olen myös ollut turhautunut niiden tyypillisistä heikkouksista. Joskus tehtävänanto on epämääräinen, toisinaan taas ratkaisuvaihtoehtoja on selvästi enemmän kuin tehtävän laatinut henkilö on tajunnutkaan. Mikä onkaan raivostuttavampaa kuin keksiä selvästi oikea vastaus, mutta mielikuvitukseltaan rajoittunut pulmanikkari kelpuuttaa vain yhden vastauksen, joka on jokin aivan toinen.

Ehkä ärsyttävimmällä tavalla puutteelliset pulmat löytää somesta tai iltapäivälehdistä tähän tyyliin:

Kahden ensimmäisen rivin perusteella useimmat päättelevät minun laillani, että banaani= 5 ja omena = 3. Moni varmaan antaa kolmannen rivin kysymykseen vastaukseksi 13, jota tehtävän laatijakin on luultavasti tarkoittanut. Tämä on loogisesti hyväksyttävä vastaus, mutta ei todellakaan ainoa.

Pysähdytäänpä hetkeksi miettimään, mitä käytetyillä symboleilla tarkoitetaan. Toisin sanoen, onko kuva banaanista eli banaani yhtä kuin luku 5, tarkoittaako se numeromerkkiä 5, vai onko se sittenkin muuttuja? Nämä kolme vaihtoehtoa nimittäin johtavat eri vastauksiin.

Ensimmäinen vaihtoehto tulikin jo käsiteltyä, nyt on toisen vuoro. Jos banaani tarkoittaa numeromerkkiä 5, silloinhan kaksi banaania eli banaani banaani = 55, ja vastaus kolmannen rivin kysymykseen on 58.

Entä jos kyseessä onkin tapa merkitä muuttujia symboleilla? Tällöin on syytä huomata, että muuttujien välisissä kertolaskuissa jätetään usein kertomerkki pois tähän tyyliin: a * b + c = ab +c. Eli banaani banaani = 5 * 5, ja vastaus kolmannen rivin kysymykseen on 28.

Mutta hetkinen, kolmannella rivillähän banaanit eivät ole erikseen, vaan ne on piirretty tertuksi. Jospa tuo liitoskohta tarkoittaakin potenssiin korotusta eli kahden banaanin terttu = 5^5 = 3125 ja laskun vastaus on 3128. Ja paljosta vetoa, että kysymykseen tarjotaan vain yhtä oikeaa vaihtoehtoa. Aarrgghh!

Tilanne ei ole oleellisesti selkeämpi myöskään tehtävätyypissä, jossa järjestyksessä luetellun joukon alkioihin pitäisi lisätä seuraava, toisin sanoen päätellä kaava, jolla esim. lukujonon jäsenet määritellään. Otetaan äärimmäisen yksinkertainen esimerkki: 1,2,4,8,16,…

Toisin sanoen seuraava jäsen vaikuttaa olevan edellinen kerrottuna kahdella, tämän saa esimerkiksi lukujonosta

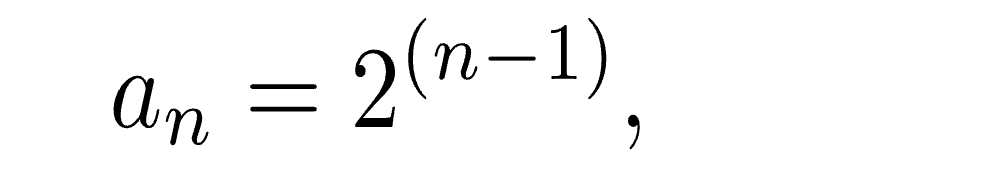
missä n=1,2,3,...

Tässä tapauksessa a₆ =32, vastaus jonka useimmat antavat ja joka tehtävän laatijallakin lienee ollut mielessä. Mutta yhtä loogisesti se voisi olla 31. Ai miten niin?

Entä jos lukujonon määräävä kaava onkin jokin toinen, sellainen joka antaa ensimmäisissä viidessä tapauksessa samat numerot, mutta eroaakin lukujonon kuudennen jäsenen kohdalla. Tämä onnistuu esimerkiksi kaavalla

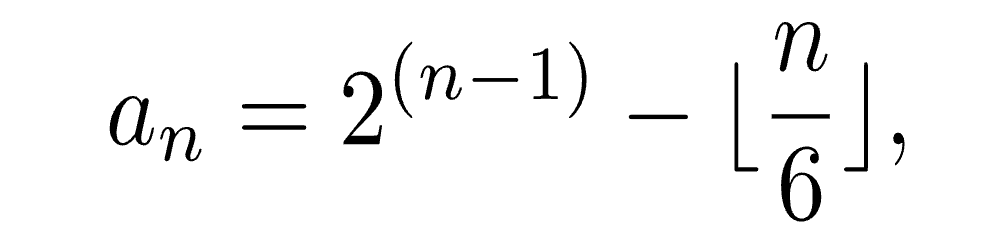
missä erikoinen sulkumerkintä tarkoittaa kokonaisosan ottamista sisällään olevan laskutoimituksen tuloksesta. Niin kauan kuin n < 6, se on 0, mutta kun n on välillä [6,11], se saa arvon 1, kun n = 12, se onkin 2 ja niin edelleen, idea tuli varmaankin selväksi. Vastaavalla tavalla voi konstruoida äärettömän määrän lukujonoja, joissa on samat viisi ensimmäistä jäsentä.

Tässä vaiheessa joku varmaankin huomauttaa, että tehtävän ratkaisijan täytyy hoksata, että nyt haetaan mahdollisimman yksinkertaista ratkaisua. Mutta miksi ihmeessä – onko meillä mitään takeita siitä, että tilanteet reaalimaailmassakaan ovat sellaisia? Occamin partaveitsi ruostuu nopeasti tylsäksi joutuessaan sateelle alttiiksi.

On myös syytä huomata, että vastaukseen a₆ = 31 voi päätyä myös jokseenkin yhtä yksinkertaisella, mutta tyystin erilaisella tavalla kuin ensimmäisen kaavan lukujono. Ehkä luvut ovatkin vastauksia yksinkertaiseen geometriseen ongelmaan: jos jonon järjestysnumero n vastaa ympyrän kaarelle piirrettävien pisteiden lukumäärää, ja jonon alkio ilmoittaa kuinka moneen osaan pisteet toisiinsa yhdistävät viivat ympyrän alan enimmillään jakavat?

Yhden pisteet tapauksessa jakoviivoja ei tule lainkaan, joten vastaus on ilmeinen yksi, kahden pisteen tapauksessa osia on korkeintaan kaksi (pisteet voivat olla myös samoja, tätä ei ole säännöissä kielletty). Entä kun pisteitä on enemmän? Seuraavat kolme tapausta ovat lupaavia:

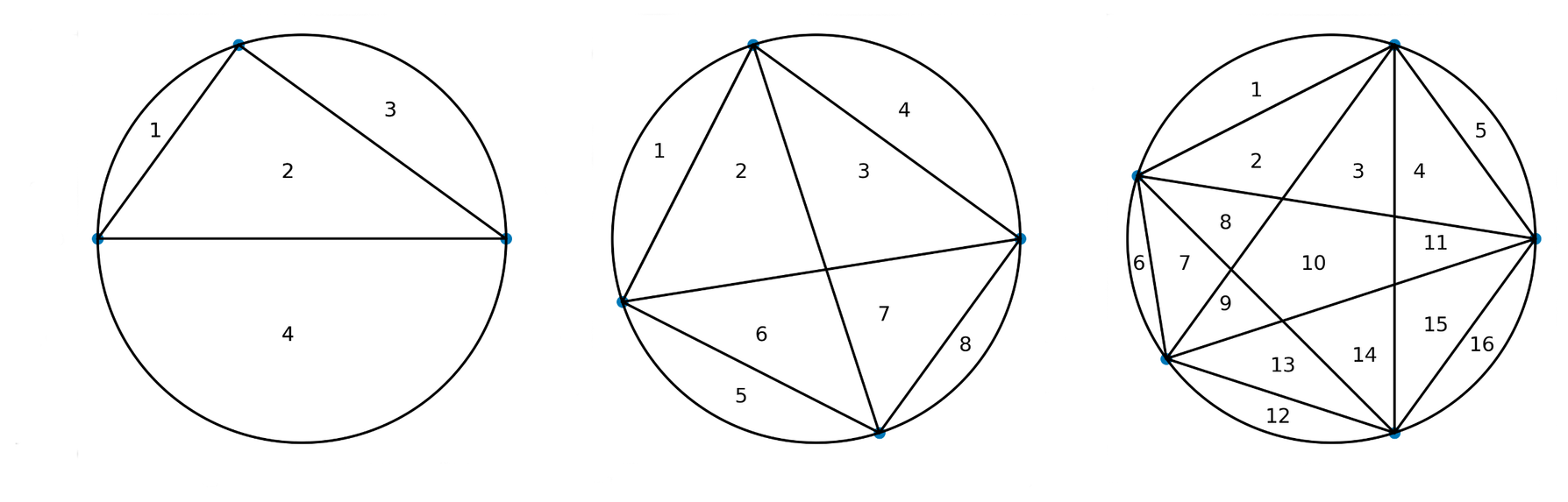
Kun pisteitä on kehällä n=3 kappaletta, ympyrän ala jakaantuu korkeintaan neljään osaan, neljällä pisteellä saadaan osien lukumääräksi 8 ja viidellä pisteellä 16, eli aivan kuin lukujonossa. Mutta mitä tapahtuu, kun pisteitä onkin n=6 kappaletta?

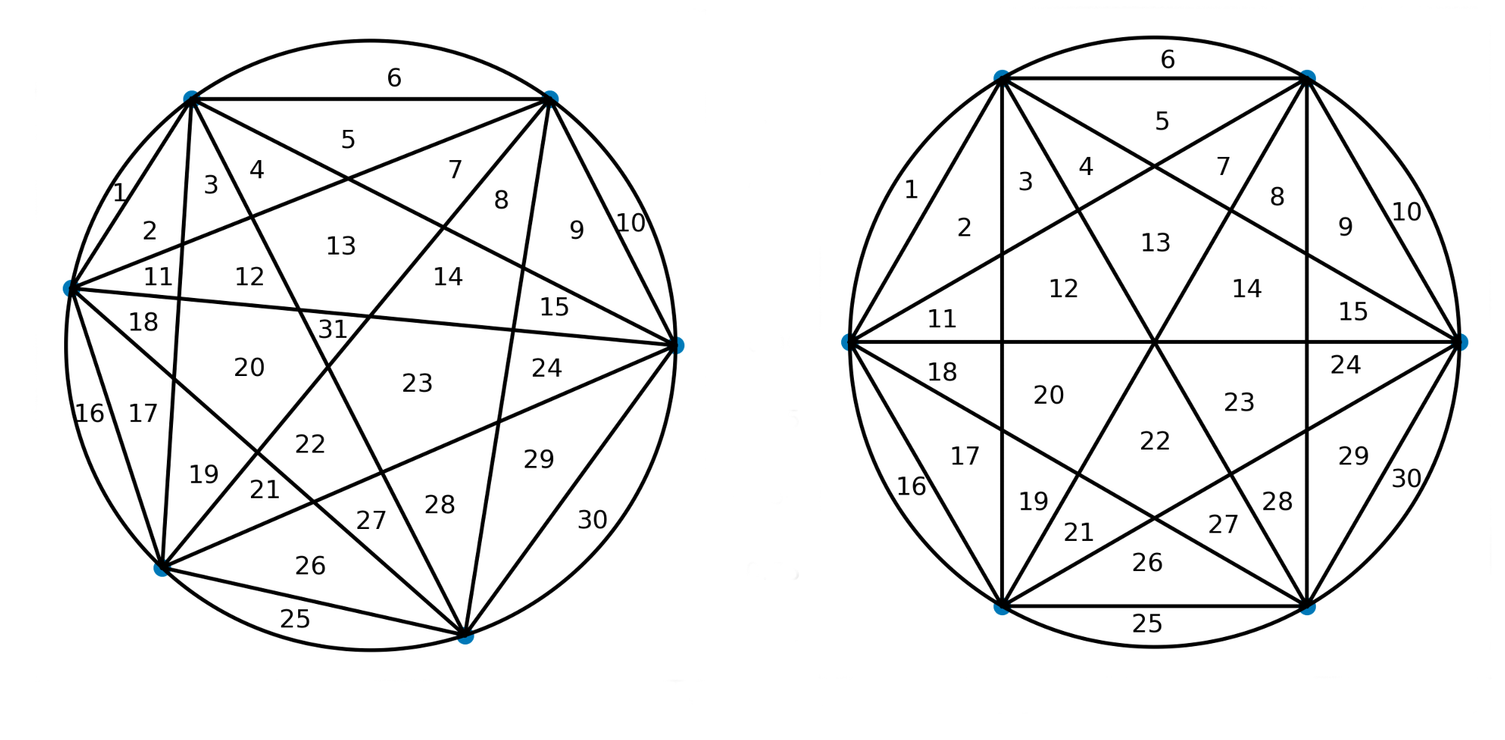
Yleisessä tapauksessa ympyrän osa-aloja onkin nyt 31 kappaletta, ja jos pisteet ovat jakaantuneet tasaisesti pitkin ympyrän kehää, niitä on 30!

Edellä kuvailtu geometrinen ratkaisu lukujonon takana ei ole mielestäni yhtään sen monimutkaisempi kuin luvun 2 potensseihin perustuva ja voi olla monen mielestä jopa helpompi ymmärtää.

Joka kerta kun törmään edellisten kaltaisiin ongelmiin ratkaisemissani tehtävissä, vannon, etten enää koskaan tuhlaa aikaani moisilla pähkinöillä, ties millä lisäaineilla ovat kasvatettuja. Mutta sitten sorrun taas, huomaan jättiläislaiskiaisen kokoisen aukon tehtävänannossa ja minua ketuttaa kuin pientä oravaa. Mansikka + omena = spiraaligalaksi.

Pertti Rautiainen on koomikko, kirjailija, runoilija ja entinen tähtitietelijä. Hän julkaisee itsekirjoittamiaan vitsejä Verde viihteellä -palstalla.